有人想要跟陌生人交換禮物嗎 ?

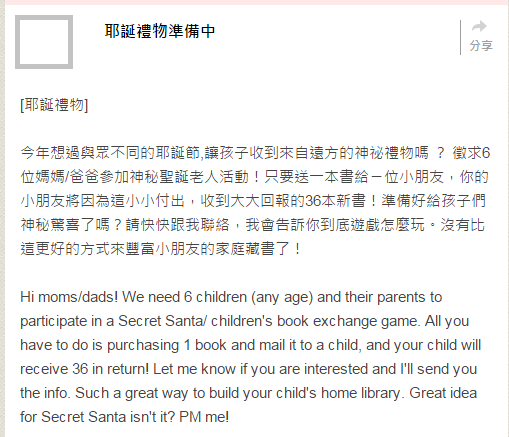
最近 Facebook 上出現一種 “有人想要跟陌生人交換禮物嗎” 的活動，大概因為我的人緣不算太差，我也看到好幾個不同的版本。有 “這是一個只屬於女生的秘密交換禮物活動”，也有 “送書給小朋友活動”。不過他們共同的特點就是，不管是送出一份價值 100 元以內的禮物，還是一本童書，玩遊戲的人都宣稱你可以收到 6 到 36 份不等的禮物做為回報。

一比六到一比三十六 ? 有這麼好康的事 ? 這是賣腎嗎 ?

遊戲規則

這些遊戲的規則都一樣: 你會從邀請你玩遊戲的人 (就是你的上線) 拿到一個地址，你要把你送出的禮物寄給他。然後呢，你要找 6 個人參加遊戲 (就是你的下線)，把你上線的地址給他們，並告訴他們遊戲規則: 乖乖寄禮物到這個地址。同時你的下線們也會拿到你的地址，但是他們並不需要寄禮物給你，而是再繼續去找下線，並把你的地址傳下去。

聽起來有點複雜喔 ? 那我們畫個圖來解釋好了。

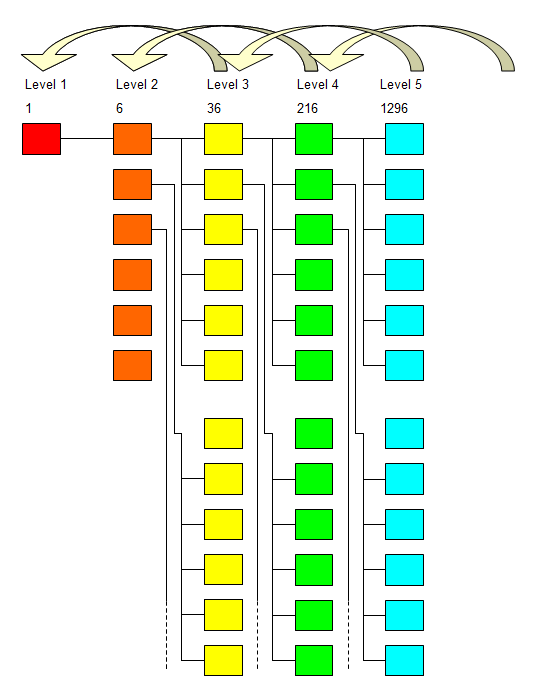
由於遊戲規則要求每個人去找六個人參加遊戲 (事實上原文的說法是 “限六個人”，製造一種限量就是殘酷的印象讓下線自動上勾)，所以如果第一層是一個發起人的話，第二層就是 6 個人，第三層就有 36 個人，第四層就已經有 216 個人。擴散的速度非常可怕。

而寄送的規則是，你要寄東西給你上線的上線。由於上線的上線是你朋友的朋友，因此你不見得認識他。這會讓你覺得你是在寄禮物給陌生人，而不是自己的朋友。同樣的，你也會收到從你的下線的下線而來的禮物，你不一定認識他，因為他也是你朋友的朋友，所以你也會覺得是在跟陌生人交換禮物。

倍增的力量

我好像聽過哪個直銷公司講這句話，對，倍增的力量，一變六到三十六就是從這裡來的。

如果你乖乖找了 6 個下線，而這 6 個下線也都找了 6 個下線，你就會有 36 個下線。根據規則，這 36 個下線就是會寄禮物給你的人，所以如果你的下線很夠力，每一個都能完美達成認務，你就會收到 36 份禮物。

如果你的下線辦事不力，每個下線都只能找到 1 個人讓遊戲繼續下去，那你就只有 6 個下線的下線。我猜這是原來發起的人所設定的最壞狀況。當然事實上還有可能更糟。

但這個遊戲的關鍵就是，你必需找到下線，然後你的下線又得找到下線，你才收得到禮物。

而每個人往上兩層寄送禮物時，並不會知道有多少人跟他一起寄送禮物給同一個人 (完美的例子是 36 人)，因此寄送禮物的人也有一種 “我不過就是送了一份禮物出去” 的感覺。

龐氏騙局

有沒有人會收不到禮物呢 ? 理論上來說，如果這個遊戲不斷地擴散下去，每個人都找得到 6 個下線以及 36 個下下線，好像就可以一直玩下去。直到有人找不到下線為止。

6 其實是一個很可怕的數字，我們剛剛算過玩到第 5 層就已經有 1296 個人了，事實上玩到第 10 層就已經 10,077,696，也就是一千多萬人了，而到 13 層就已經超過地球的人口了。(“倍增的力量”，huh?)

先不管到底照這樣的擴散方式有沒有辦法觸及地球上所有的人，光是你身邊的人願不願意加入，以及會不會邀請到已經成為別人下線的人，就已經是很大的問題。

Anatol Rapoport 的 “小世界理論” 將人與人之間的連結分成強連結和弱連結，當小世界網路需要擴展以觸及遠方的對象時，弱連結扮演了關鍵的角色。這個遊戲要玩得下去，一定要有弱連結參與，否則照 6 的 n 次方這種擴散速度，你朋友圈中的強連結很快就被耗盡了。結果就是你會發現你身邊的人每個人都已經寄了一份禮物出去了，但是你還收不到禮物。

這是一個很典型的龐氏騙局: 利用後期投資者的資源繳給前期投資者，以換取不合理的回報。三十六份禮物就是一個不合理的回報，因為你只送出一份。

我覺得一開始發起遊戲的人太貪心，選了 6 這個數字。他也許是希望這個遊戲能快速擴散，但結果卻有可能是快速耗盡小圈圈中的強連結，而無法立用弱連結擴散到遠方。我覺得 2 就已經是個很貪心的數字了，因為如果用 2 來玩，你會收到 4 份禮物。一比四，仍然是個很不合理的數字。

如果用 1 來玩，玩得下去嗎 ? 應該也是可以的，而且這會變成一個很公平的遊戲: 付出一份、得到一份。但中間不能有任何差錯，只要有人不玩，線就斷了。

所以，你想要跟陌生人交換禮物嗎 ?

推鑑閱讀

推鑑一下這本書 “連結”。它從我們常聽到的 “六度分隔理論” 開始，說明了各種不同的連結模型以及小世界的理論，有些很直覺，有些卻跟我們的直覺背道而遲。很有意思的書，網路時代你不可不知的一些模型都在裡面了。

(我其實有點懷疑，發起這個遊戲的人選擇 6 這個數字，是不是因為他誤解了六度分隔理論的意思 ? 鄉親啊，六度分格的六是 “六層”，不是 “六個人” 啊…)